Using the binary search takes less time than a linear search. In this article, I explain binary search with typescript based on my learning
What is the working principle of the binary search?
One prerequisite, or one requirement for the binary search, is that the Array of data must be sorted. If array data is not sorted, you can’t apply binary search. So you need to sort data first then you can apply
An essential point of binary search is Divide And Conquer Technique, What are the means? It’s going to divide the array into two halves recursively. Imagine the scenario we have a sorted array and we need to search 56 data-position/index of the array. So our target value is 56.
Let’s explain,
// Array const arr: number[] = [3, 7, 9, 13, 14, 45, 56, 78, 89, 100];
We will take three variables, the first left variable which is starting of the array, Then right variable which is the end of the array, and the mid variable which is the middle of the array. Then we recursively condition-wise update those variables until we found our target data or check over the array data.
- Case 1: target === arr[mid]; return index/position
- Case 2: arr[mid] < target; update left pointer to mid plus one and midpoint to the center
- Case 3: arr[mid] > target; update right pointer to mid minus one and midpoint to the center
Note: Sometimes we will get mid value as a decimal. when we get the decimal value we convert it to floor value, Check out what is floor value.
Loop/Recursive Explain
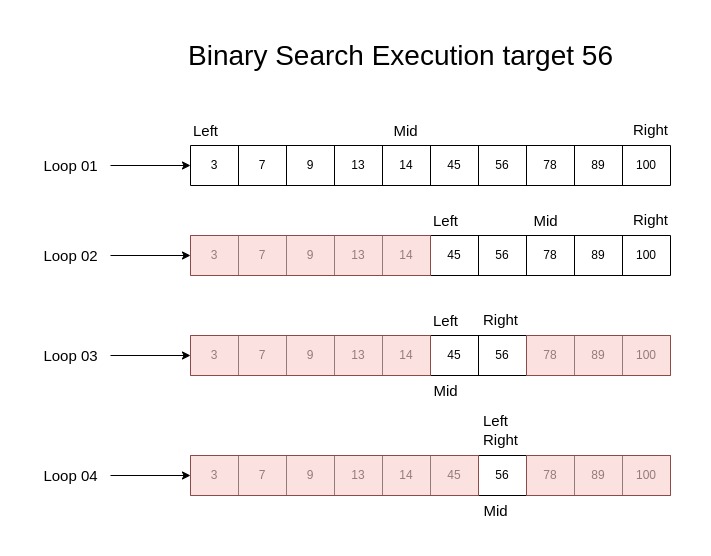
So at the start, we have left 0, right 9 which is the end index of the last element, and row mid is 4.5 which is the floor value is 4.
| No. | Left | Right | Mid |
| 01 | 0 | 9 | 4 |
| 02 | 5 | 9 | 7 |
| 03 | 5 | 6 | 5 |
| 04 | 6 | 6 | 6 |
- Loop 01: In the very first loop execution mid index 4 means in index 4 data is 14, And 14 is less than the target value 56. That meets Case 2, So the target value does not exist in the left to mid-sub-array. So We need to update the left pointer to mid plus one and update the mid pointer base one new sub-array. Now the left pointer is 4+1=5 and the mid is 7
- Loop 02: Now mid-index data is 78. 78 is greater than our target data 56. That meets our case 3. So we need to update the right pointer to mid minus one. Now the right pointer is 7 – 1=6 and the mid is 5.
- Loop 03: Now mid-index data is 56, and 56 is also less than our target data 56. Again it meets case 2. So we need to update the left pointer to mid plus one. Now the left pointer is 5+1=6.
- Loop 04: Now the mid-index data is 56, And that is our target data. So that will break the loop and return the index
So What will happen if the target value does not exist in array? If data is not found it will simply return a -1 value.
Checkout example binary search method is provided below.
Example 01. Find Index From Sorted Array
Binary Search Function TypeScript Code
/*
*
* Time complexity: O(log n)
*
* Space complexity: O(1)
*
*/
function findIndex(arr: number[], target: number): number {
let left: number = 0,
right: number = arr.length - 1,
mid!: number;
while (left <= right) {
mid = Math.floor((left + right) / 2);
if (arr[mid] === target) return mid;
if (arr[mid] < target) left = mid + 1;
else right = mid - 1
}
return -1
}
Execute Search Function
const arr: number[] = [3, 7, 9, 13, 14, 45, 56, 78, 89, 100]; console.log(findIndex(arr, 9)) // Return 2 console.log(findIndex(arr, 78)) // Return 7 console.log(findIndex(arr, 50)) // Return -1
Example 02. Find Position in Rotated Sorted Array
/*
*
* Time complexity: O(log n);
* Space complexity: O(1);
*/
function findPosition(nums: number[], target: number): number {
let start: number = 0, end: number = nums.length - 1, mid!: number;
let startVal!: number, midVal!: number;
while(start <= end) {
mid = Math.floor((start + end) / 2)
midVal = nums[mid];
if (midVal === target) return nums.indexOf(target);
startVal = nums[start];
if (startVal <= midVal) {
if (startVal <= target && target <= midVal) end = mid - 1;
else start = mid + 1;
} else {
if (midVal <= target && target <= nums[end]) start = mid + 1;
else end = mid - 1;
}
}
return -1
};
const arr = [4,5,6,7,0,1,2]
console.log(findPosition(arr, 0)) // return 4
console.log(findPosition(arr, 3)) // return -1
console.log(findPosition(arr, 6)) // return 2